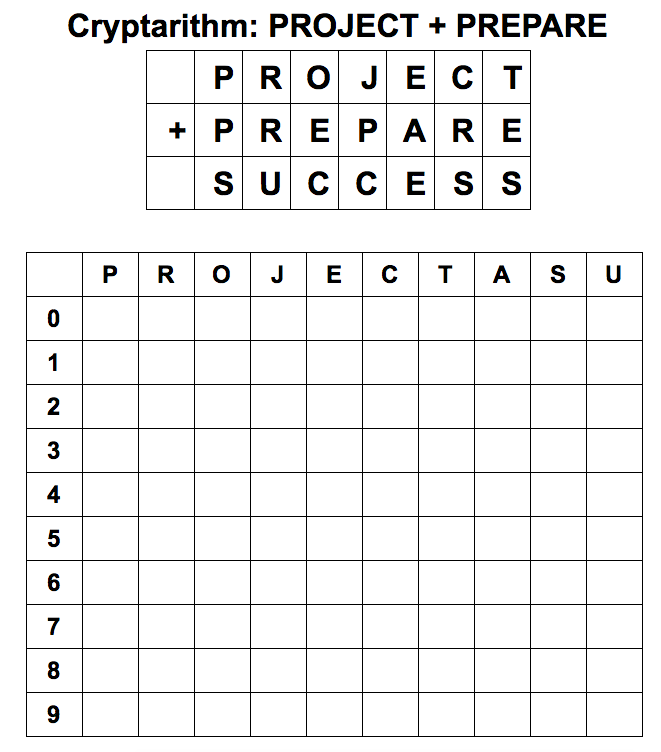
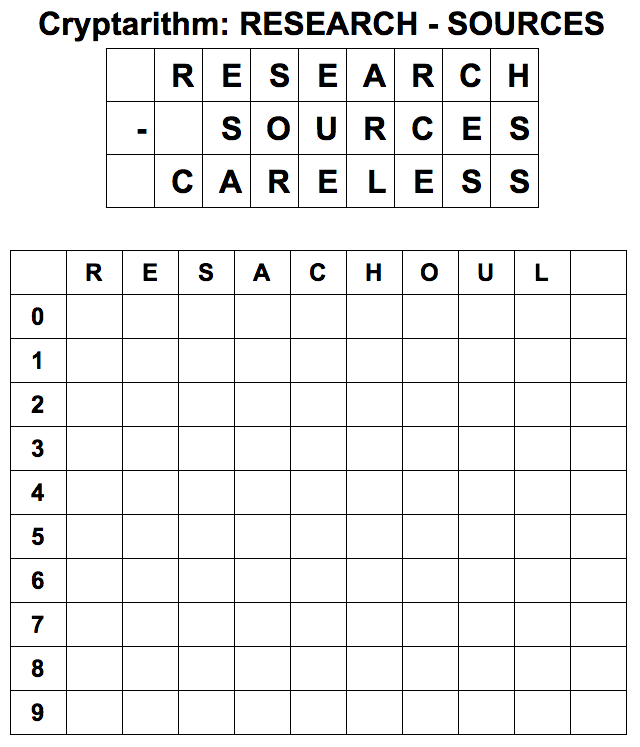
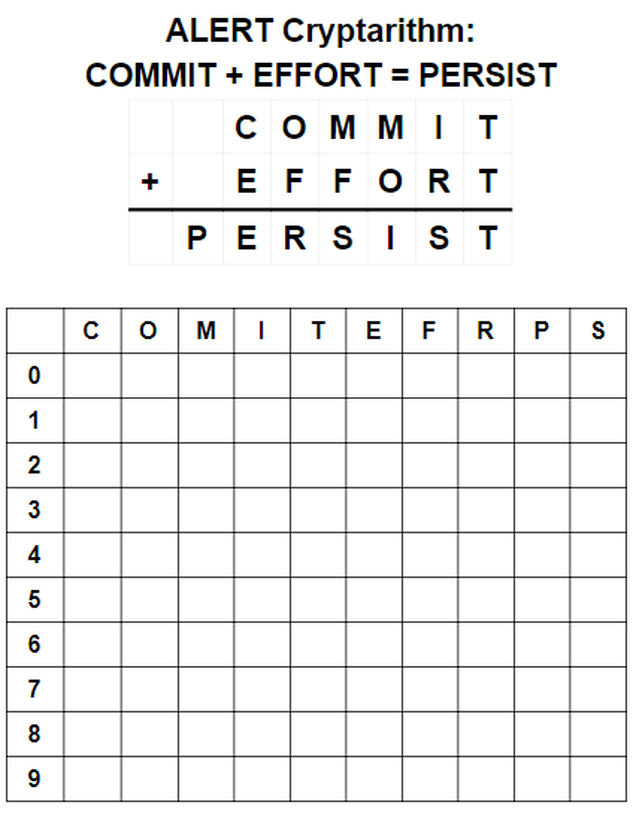
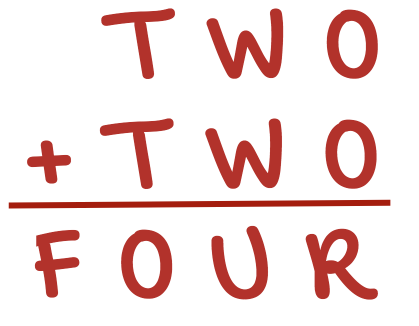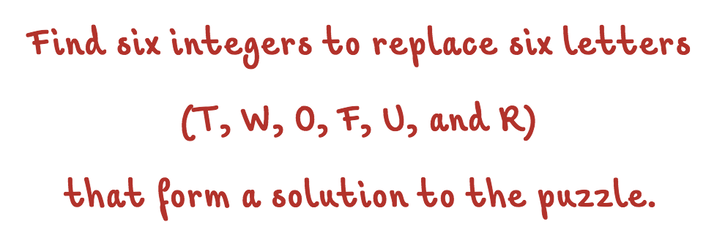Cryptarithms
A cryptarithm is a math puzzle or a math riddle wherein the digits 0 through 9 are replaced by letters to form a substitution cypher.
Any addition, subtraction, multiplication, or division problem can become a cryptarithm by replacing the numbers with letters, but the ones that students and puzzle hunters seem to enjoy the most are those that use words that are connected in some way. At the Citadel in Charleston, the math instructor Professor Trautman uses Animal Cryptarithms to teach the cadets critical thinking and persistence.
Coaching
Set Up: Understand the problem.
- What are you asked to find or show?
- Can you restate the problem in your own words?
- Is there enough information to enable you to find a solution?
Tools: Plan your approach by choosing an appropriate strategy.
- Act It Out—use physical objects or models to represent the problem.
- Choose an Operation—what sort of arithmetic is called for (addition, subtraction, multiplication, division) by the problem?
- Guess and Check—when there is more than one variable involved, control one variable to test what combinations will result in a solution.
- Look for a Pattern—Do you see a repeated relationship between numbers in the problem?
- Make a Chart or Table—when many combinations of numbers or objects are possible, a chart or table helps illustrate the possibilities.
- Make a Drawing or Diagram--can you draw a picture or a diagram that might help you understand the problem?
- Solve a Simpler or Similar Problem—have you seen a problem like this before? How did you solve it?
- Use Logical Reasoning—a set of statements often creates a problem with a limited number of solutions (or only one).
- Work Backwards—If an answer is given, can you reverse the steps in the problem to create the beginning values?
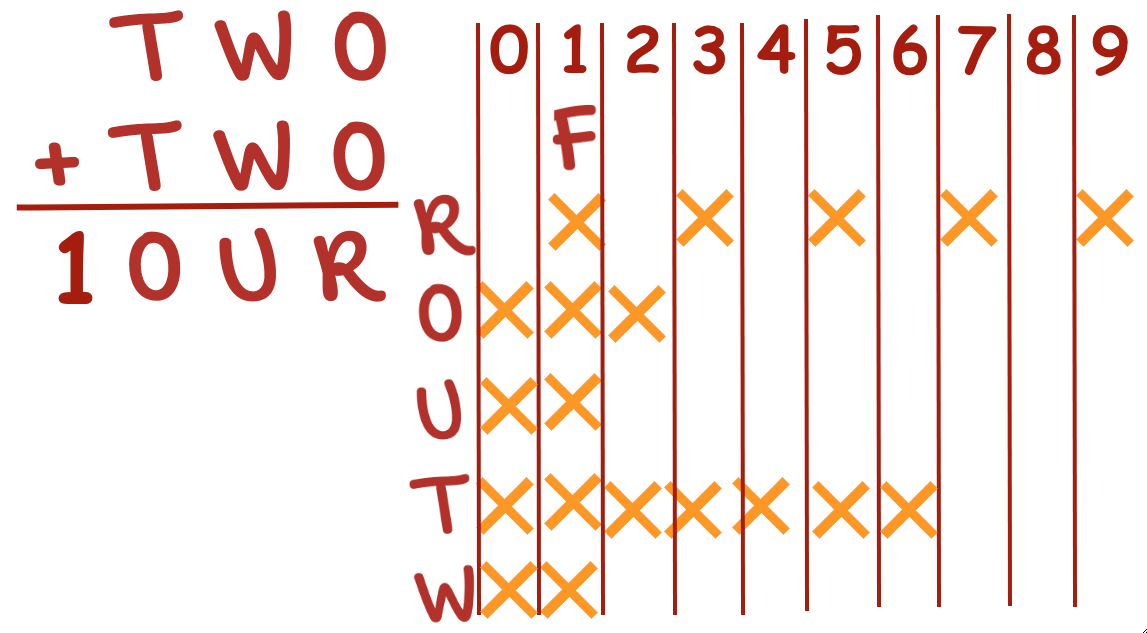
What do we know?
F must be 1 . . .
because no two addends will have a sum greater than 18 (19 with regrouping)
. . . R must be even (or 0) . . .
because two identical integers will have an even sum
. . . O cannot be 0 (zero) . . . because then R would also be 0
. . . T cannot be 0, and must be greater than 4. because having a zero as the leading place value is not a mathematical convention; and the two identical integers (with or without regrouping) must have a sum of 10 or more to have a 4-digit sum as the solution.
Act: Solve the problem.
- Persevere: Carry out your chosen strategy to completion.
- Be Precise: Use care, patience, and skills.
- Express your answer in units that make sense in terms of the problem.
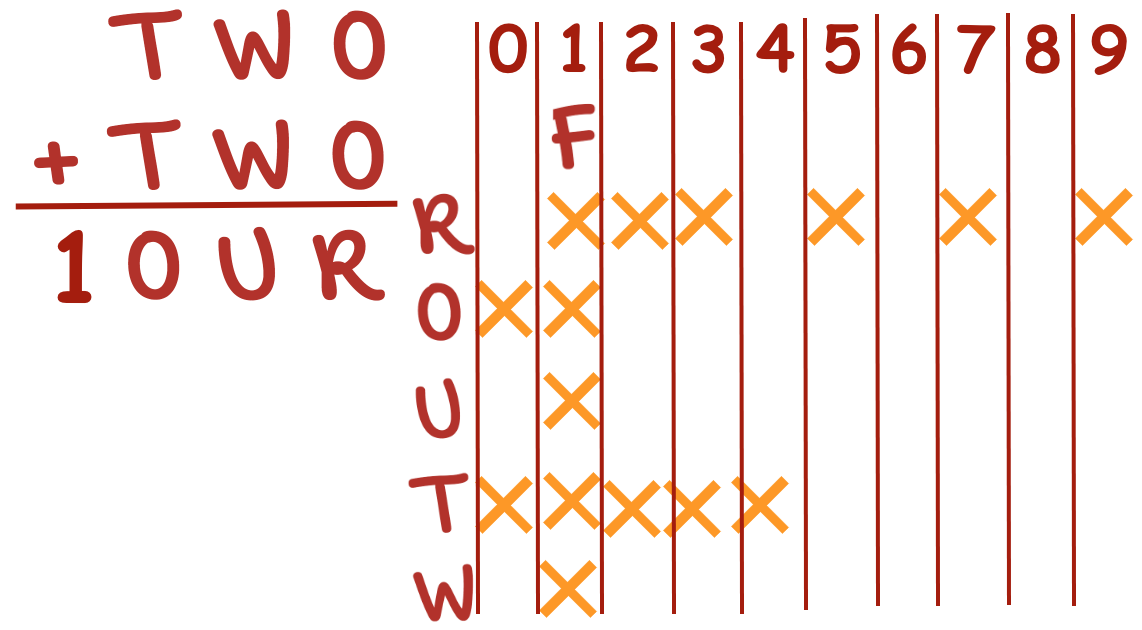
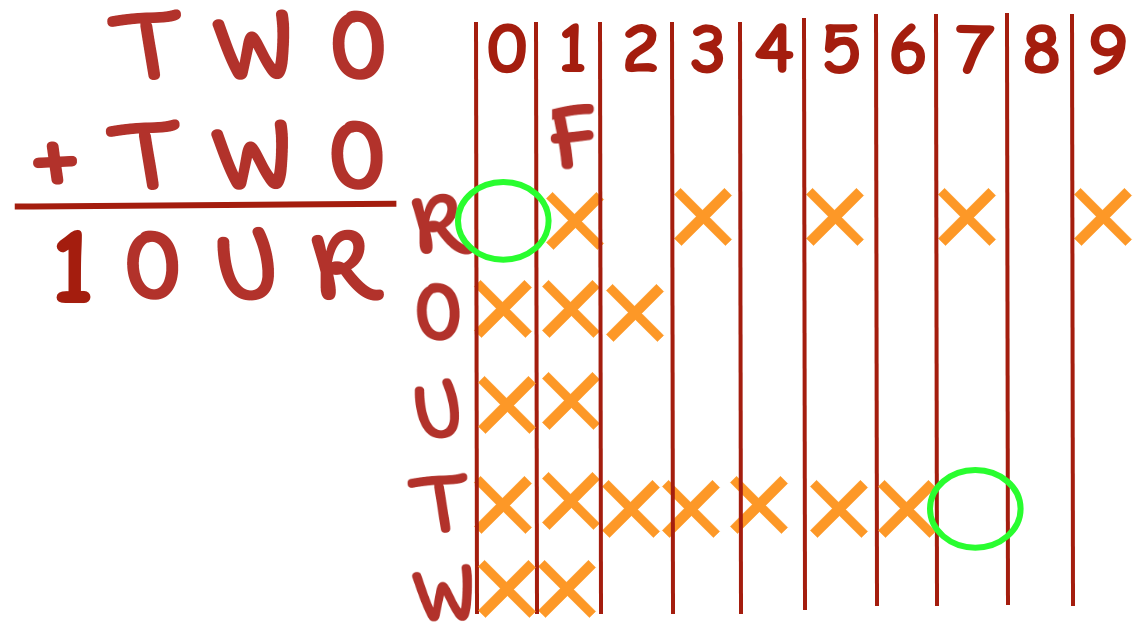
F is 1, so O cannot be 1, so R cannot be 2 (but must be even or 0) because
because two identical integers will have an even sum
. . . T cannot be 0, and must be greater than 4. because having a zero as the leading place value is not a mathematical convention; and the two identical integers (with or without regrouping) must have a sum of 10 or more to have a 4-digit sum as the solution.
Can T = 5? Guessing and checking, O would then have to be 0 or 1, making R = 0 or 2 because R = O + O, so . . . no.
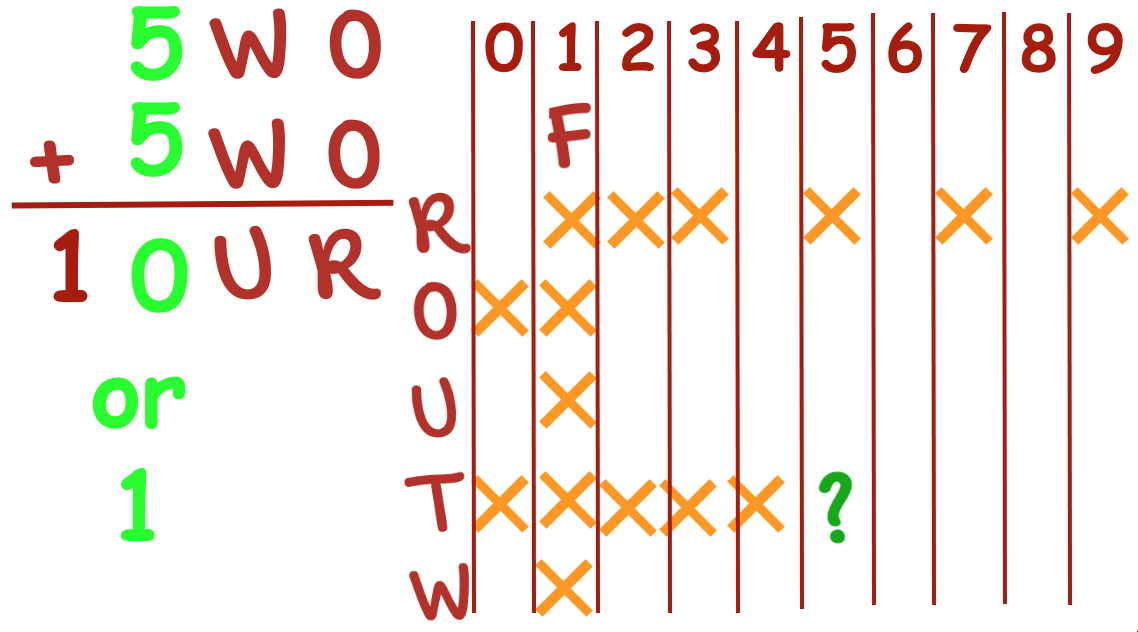
Can T = 6? O would then have to be 2, making R = 4 because R = O + O, so . . . maybe.
What would W and U have to be? W + W = U, so
3 + 3 = 6 (but 6 is already T),
4 + 4 = 8 (but 4 is already R),
5 + 5 = 10, making U = 0 (then T + T + 1 = 6 + 6 +1 = 13,
making O = 3, which is where we started with W, so . . . no. (sigh)
It seems a little discouraging, but exploring options often means closing off impossible combinations, which gets us closer to a solution.
For example, on further reflection, if W + W = U, one option we can also cross off is W = 0, because then U = 0 (or 1 with regrouping), but we cannot have W = U = 0, and we know F = 1.
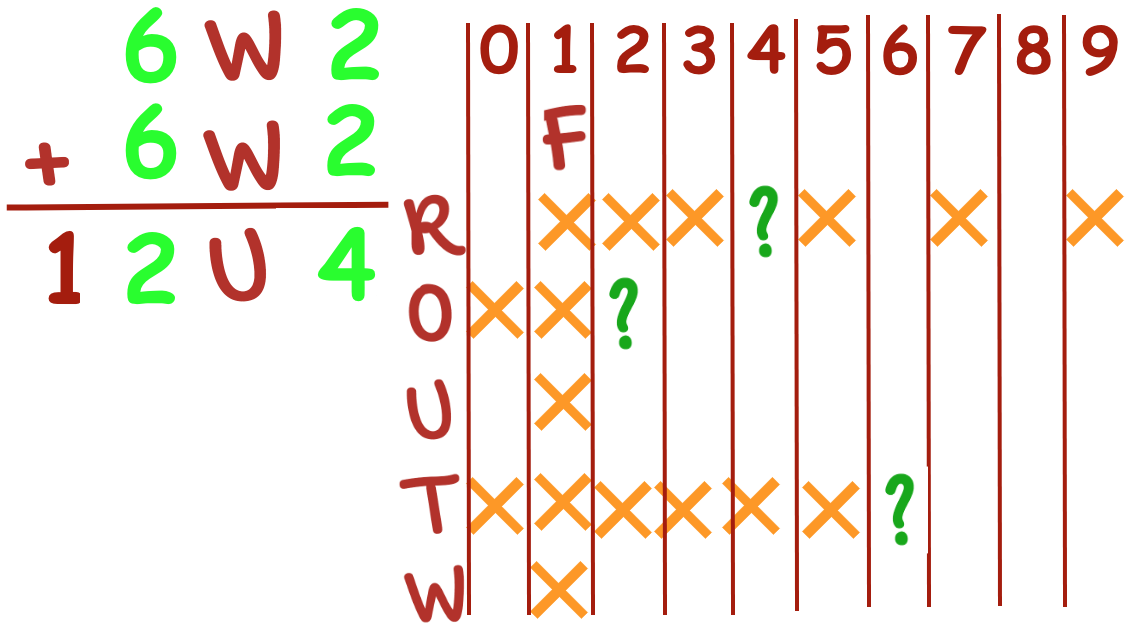
Do YOU see anything interesting?
We could explore the R = 0 (either moving forward, or closing off the option of any letter matching with 0 in this formula) or T = 7.
OR we could try BOTH. If R = 0, O must be 5; if T = 7, O could be 5 if W + W + 1 is greater than 12.
Reflect: Look back and analyze the result.
- Does your answer make sense?
- Can you explain your reasoning?
- Are there other possible solutions you overlooked?
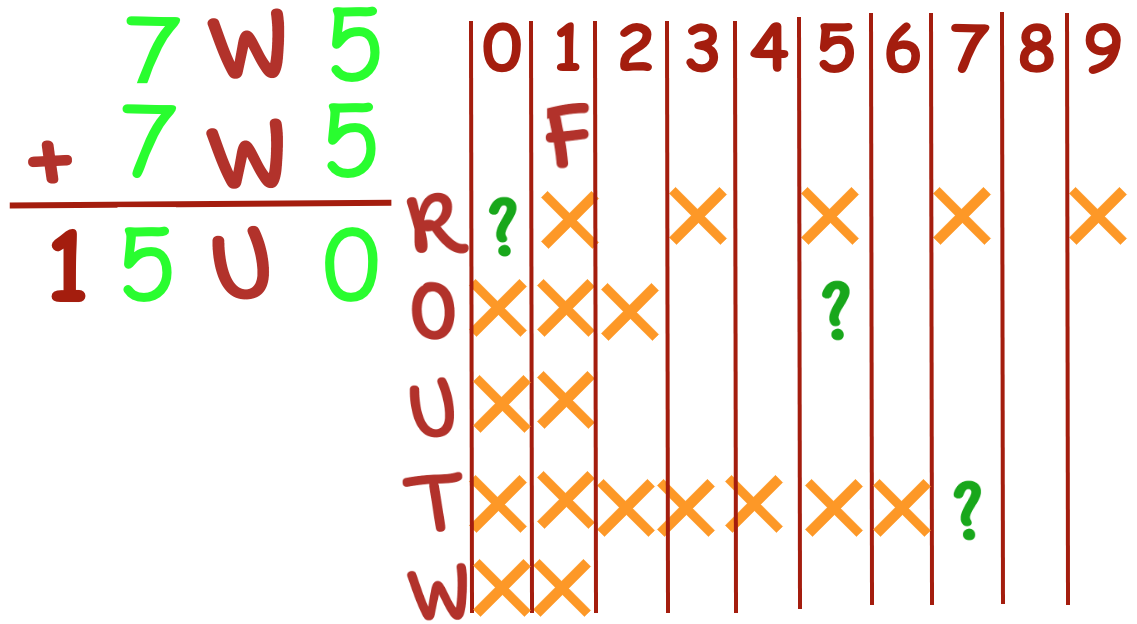
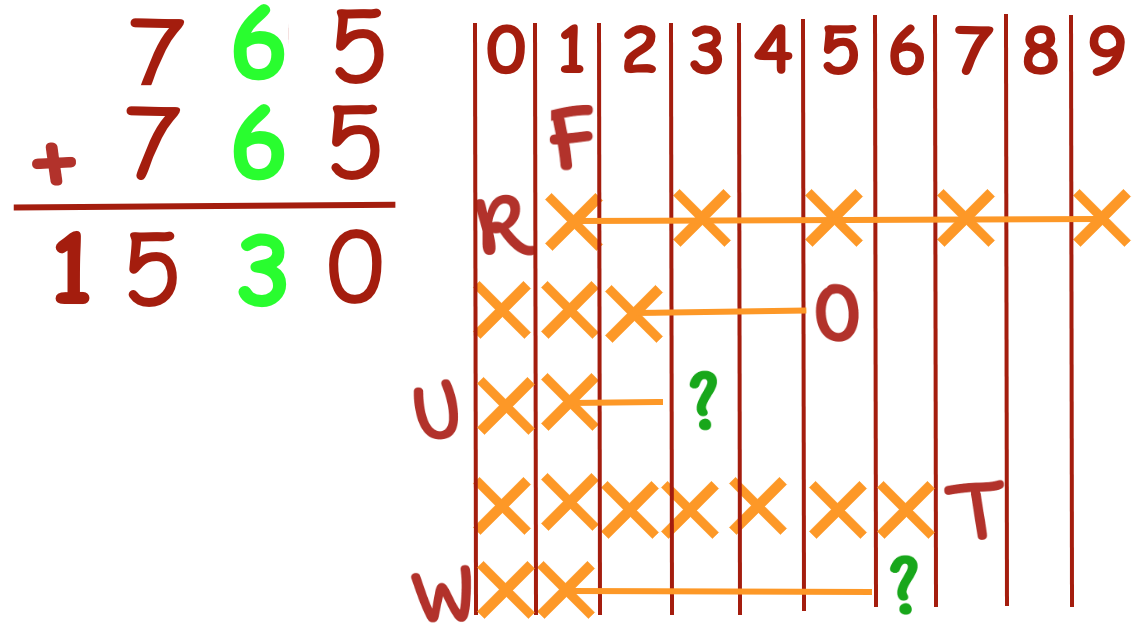
Does this solution work for the formula? Yes, it does.
Are there other possibilities? Once we find one solution, we may see more possibilities. This cryptarithm has 7 known solutions.
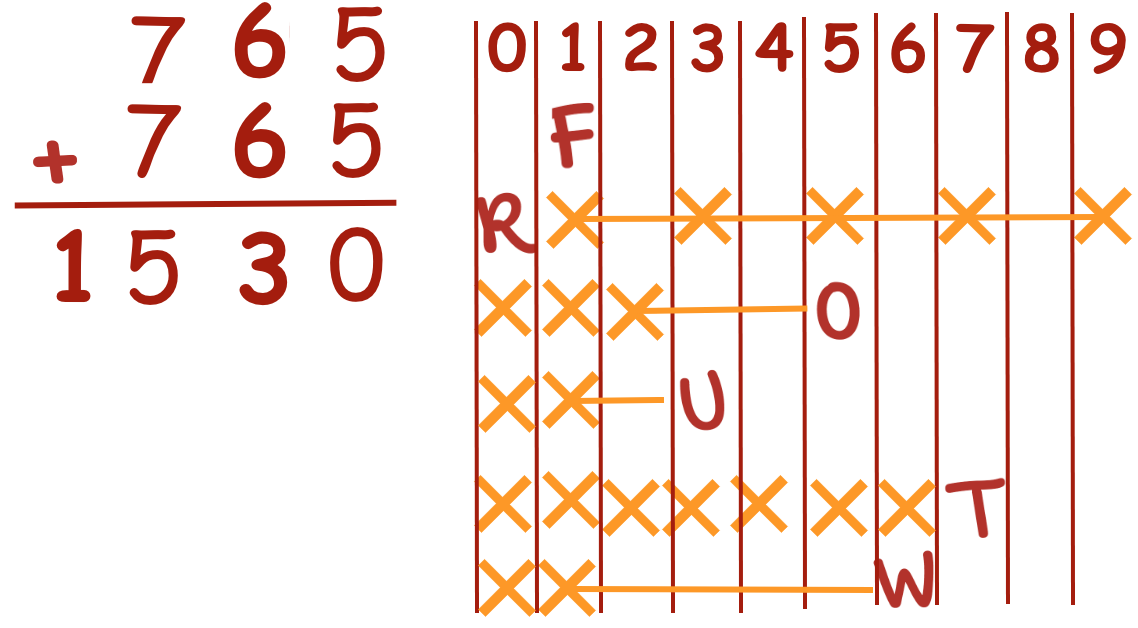
TWO + TWO = FOUR
734 + 734 = 1468
765 + 765 = 1530
836 + 836 = 1672
846 + 846 = 1692
867 + 867 = 1734
928 + 928 = 1856
938 + 938 = 1876