A History of Numbers
Natural Numbers
The first use of the concept of numbers in the historical record is their use in counting, or representing the count of, other physical objects or phenomena. In mathematical discussions, it is now customary to signal the use of the counting or natural numbers as a set represented by the letter N:
N = {1, 2, 3, 4, . . .}
N = {1, 2, 3, 4, . . .}
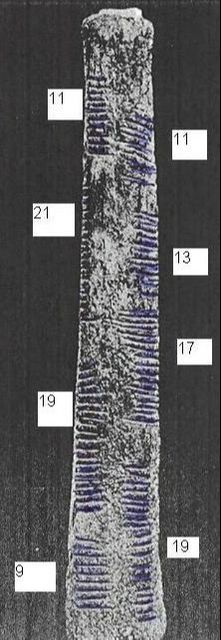
The Ishango bones are named after the place where they were found in the Democratic Republic of Congo (DRC) in 1960. The Belgian geologist Jean de Heinzelin de Braucourt uncovered the bones buried in layers of volcanic ashes on the shores of Lake Edward in the Ishango region, near the border with Uganda. The Ishango bones are 10 to 14 cm long with several incisions on each of the faces.
The marks on the bones may be evidence of the earliest recorded mathematical activity of human beings. Dating as far back as 22,000 years ago, in the Upper Paleolitic era, the Ishango bones are the dark brown leg bones (fibula) of a baboon, with a sharp piece of quartz affixed to one end for engraving. It may be the oldest evidence of the practice of arithmetic in human history.
The marks on the bones may be evidence of the earliest recorded mathematical activity of human beings. Dating as far back as 22,000 years ago, in the Upper Paleolitic era, the Ishango bones are the dark brown leg bones (fibula) of a baboon, with a sharp piece of quartz affixed to one end for engraving. It may be the oldest evidence of the practice of arithmetic in human history.
The first bone has been subject to a lot of interpretation. The second bone is broken, but has a similar pattern of notches, although it is difficult to draw conclusions because the piece is incomplete. The first bone is photographed in color above and rotated to show the sides.
|
The left column is divided into 4 groups of notches--11, 21, 19, and 9 notches, with spaces in between. Together, they add up to 60 notches.
At first, it was thought to be just a tally stick with a series of tally marks, but scientists have demonstrated that the groupings of notches on the bone are indicative of a mathematical understanding which goes beyond simple counting. Jean de Heinzellin was the first to consider the bone as an exploration of patterns in numeration: the numbers in the left column were compatible with a numeration system based on 10, since he saw that: 21 = 20 + 1, 19 = 20 – 1, 11 = 10 +1, and 9 = 10 -1. |
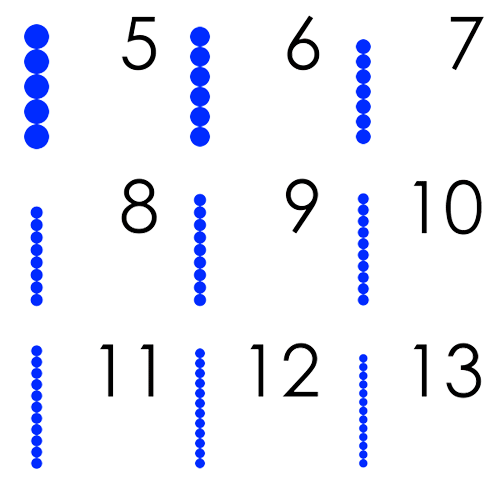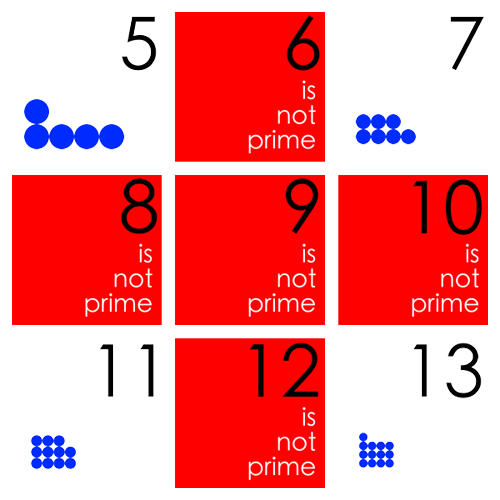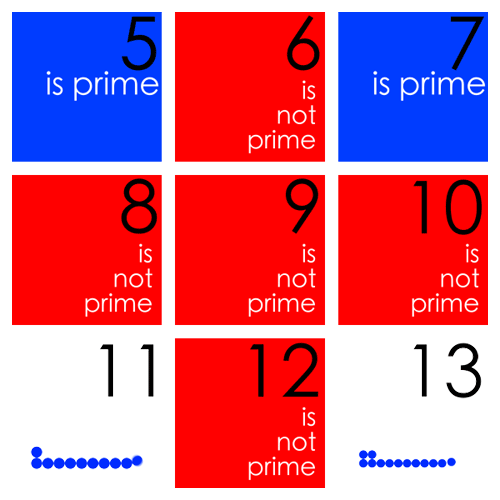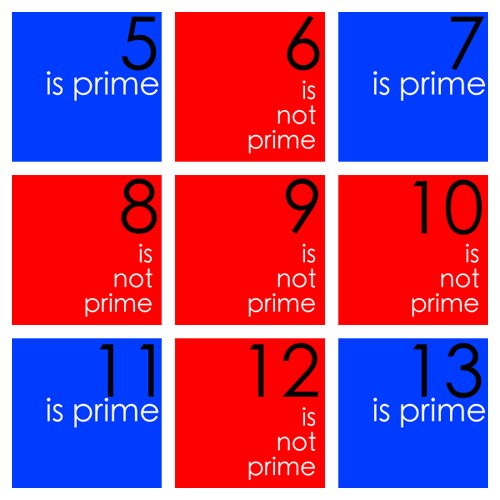
The right column can be divided in groups of 11, 13, 17, and 19 notches. These are the prime numbers between 10 and 20, and the sum of these is also 60.
In fact, many believe that the notches follow a preplanned mathematical pattern using the primes. The notches have been interpreted as a prehistoric calculator, a lunar calendar, or a seasonal record.
|
Egyptian Hieroglyphic Numbers
Egyptian Binary (base 2) Number Methods
Maya Vigesimal (Base 20) Numbers
No counting method seems quite as natural to us as that of holding up or turning in each finger, and since we have 10 fingers the decimal (base 10) system is the most common in human cultures.
The reason Maya numerals were vigesimal (20-base) is also anatomical. We have 10 fingers and 10 toes. Each limb (hand or foot) can count up to five and this is why many decimal or vigesimal systems include a quinary (base 5) subsystem. The figure below shows the sub-base of Maya’s vigesimal system is five, where one dot seems to represent one finger/toe and one horizon one limb.
The reason Maya numerals were vigesimal (20-base) is also anatomical. We have 10 fingers and 10 toes. Each limb (hand or foot) can count up to five and this is why many decimal or vigesimal systems include a quinary (base 5) subsystem. The figure below shows the sub-base of Maya’s vigesimal system is five, where one dot seems to represent one finger/toe and one horizon one limb.
Babylonian Sexagesimal (Base 60) Numbers
Sexagesimal is a numbering system whose base is sixty. It originated with the ancient Mesopotamians in the 3rd millennium BCE. It is still partially used for measuring time and angles. The numeral system we now usually use is the decimal (10-base) system and the number 123 is equivalent to 1×102+2×101+3×100, while 1 hour, 2 minutes and 3 seconds is equivalent to 1×602+2×601+3×600=3723 (seconds).
A popular hypothesis first proposed by Theon of Alexandria (~405 CE) is that Sumerians valued 60 because it has many divisors. To be sure it has 12 divisors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 and it is easy to reduce a fraction with 60 its denominator.
60=1×60, 2×30, 3×20, 4×15, 5×12, 6×10
A popular hypothesis first proposed by Theon of Alexandria (~405 CE) is that Sumerians valued 60 because it has many divisors. To be sure it has 12 divisors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 and it is easy to reduce a fraction with 60 its denominator.
60=1×60, 2×30, 3×20, 4×15, 5×12, 6×10
Babylonian: Finger Counting with 60 |
Babylonian Astronomy, Angles, and Time |
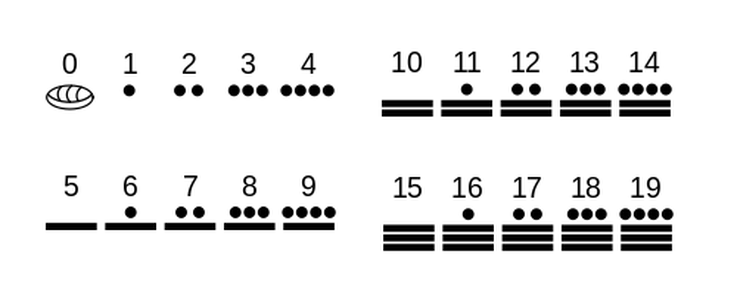
The Sumerian sexagesimal system uses ten as a sub-base. The following table indicates that the vertical wedge (V) represents 1 and the horizontal one (<) 10.
Chinese Counting Rods
Cardinal Numbers |
Ordinal Numbers |
Nominal Numbers |
|
Numbers to identify quantity.
|
Numbers to identify positions or rankings in sets or sequences.
|
Numbers to identify, label, or name objects or items.
|